یکی از مهم ترین موضوعات یعنی Belief propagation که در این جا پوشش پیدا کرده است. از چه دانشگاه هایی این مطالب را پیگیری می کنند و بعد revise خوردن و انتظار طولانی یک سال و نیم آن را در ژورنال های بین المللی elsevier نیز چاپ کردند. ما اصل مقاله را قبل revise خوردن در اختیار شما قرار دادیم لذا خلاصه مقاله را با هم بررسی کنیم و در انتهای مطلب آن را به طور کامل و به صورت رایگان دانلود کنید:
عنوان: Separate but Equal: Equality in Belief Propagation for Single Cycle Graphs
نویسندگان: Sanchit Arora, Pradeep Varakantham
منتشرشده در: Proceedings of the 32nd International Joint Conference on Artificial Intelligence (IJCAI 2023)
🎯 مسئله
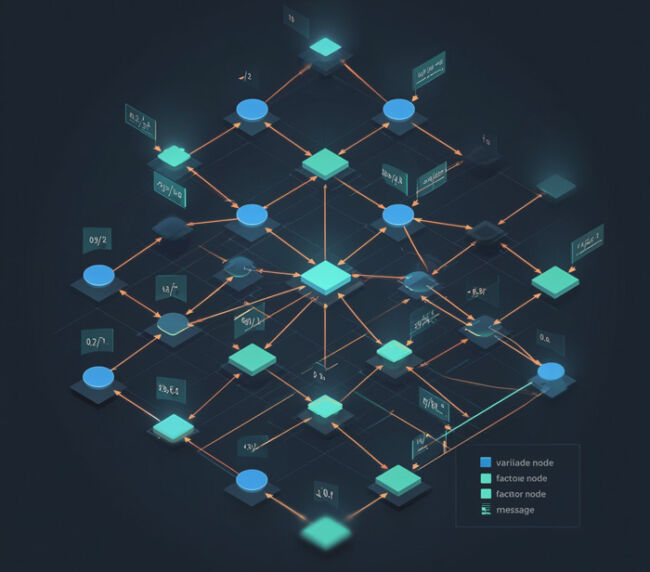
الگوریتمهای انتشار باور (Belief Propagation – BP) یکی از روشهای کلیدی در استنتاج احتمالاتی و حل مسائل بهینهسازی توزیعشده هستند.
در عمل مشاهده میشود که در برخی ساختارهای گرافی، بهویژه گرافهای تکچرخهای (Single-Cycle Graphs)، مقادیر باور در طول اجرا برابر میشوند (Belief Equality) که منجر به نوسان و عدم همگرایی الگوریتم میشود.
پژوهش حاضر این پدیده را بهصورت نظری تحلیل میکند و میپرسد:
چرا و در چه شرایطی برابری باورها رخ میدهد و آیا میتوان از آن جلوگیری کرد؟
💡 ایدهی اصلی
نویسندگان نشان میدهند که برابری در باورها ویژگی درونی الگوریتم Min-Sum BP در گرافهای تکچرخهای است، نه یک خطا یا نقص عددی.
حتی اگر محدودیتهای یکتاساز یا نویز تصادفی اضافه شود، الگوریتم تمایل دارد باورها را به سمت مقادیر برابر سوق دهد.
ایدهی کلیدی آنها استفاده از مفهوم “Backtrack Cost Tree” است تا منشأ برابریها را به ساختار بازگشتی هزینهها در گراف ربط دهند.
⚙️ روششناسی
- تحلیل رفتار الگوریتم Min-Sum BP روی گرافهای تکچرخه با دامنههای متناهی.
- اثبات نظری برای دو نوع برابری:
- برابری باورها (Belief Equality): مقادیر خروجی BP برای حالات مختلف یک متغیر برابر میشوند.
- برابری تخصیصها (Assignment Equality): چندین تخصیص مختلف در نظر الگوریتم از نظر هزینه معادلاند.
- بررسی دو حالت الگوریتمی:
- همگرا (Convergent): BP به جواب بهینه میرسد.
- نوسانی (Non-Convergent): BP در چرخهای تکرارشونده گرفتار میشود و باورهای برابر تولید میکند.
- آزمون تجربی روی مجموعهای از گرافها با اندازه و دامنههای مختلف برای بررسی فراوانی وقوع برابریها.
.
📈 نتایج کلیدی
- اگر BP در گراف تکچرخهای همگرا نباشد، پس از چند مرحله، برابری در باورها اجتنابناپذیر است.
- افزودن محدودیتهای یکتاساز (unary constraints) تنها زمانی مؤثر است که الگوریتم واقعاً همگرا شود.
- در بیش از ۹۰٪ از موارد غیرهمگرا، پدیدهٔ برابری باور یا تخصیص رخ میدهد.
- با بزرگتر شدن اندازهٔ چرخه، احتمال وقوع برابری افزایش مییابد.
- تأثیر اندازهٔ دامنهٔ متغیرها: دامنههای بزرگتر کمی احتمال برابری را کاهش میدهند اما حذف نمیکنند.
💡 اهمیت و کاربرد
| حوزه | کاربرد |
|---|---|
| استنتاج احتمالاتی (Probabilistic Inference) | تحلیل بنیادی رفتار BP در شرایط غیرهمگرا. |
| بهینهسازی توزیعشده (DCOP) | کمک به درک محدودیتهای روشهای هماهنگی چندعاملی. |
| یادگیری ساختار گرافی | شناسایی الگوهای ناپایداری در گرافهای با حلقه. |
| نظریهٔ همگرایی الگوریتمی | بازنگری در مفروضات کلاسیک دربارهٔ رفتار BP در چرخهها. |
🧠 جمعبندی نهایی
این پژوهش نشان میدهد که پدیدهٔ برابری در باورها، برخلاف تصور، یک ویژگی ذاتی الگوریتم انتشار باور در ساختارهای چرخهای است.
هیچ تنظیم جزئی یا افزودن قید سادهای نمیتواند بهطور عمومی از آن جلوگیری کند.
نتیجه، بازنگری در تئوری همگرایی BP را ضروری میسازد و چشمانداز جدیدی برای پژوهش در حوزهی الگوریتمهای استنتاج پایدار و توزیعشده ارائه میدهد.
.
دانلود کامل مقاله:

