✅ خلاصه تحلیلی مقاله
عنوان: Lifted Inference Beyond First-Order Logic
نویسندگان: Sagar Malhotra, Davide Bizzaro, Luciano Serafini
منتشر شده در: Artificial Intelligence Journal (Elsevier), جلد 342، سال 2025
DOI: 10.1016/j.artint.2025.104310
🎯 هدف پژوهش
این مقاله به توسعهی نظریهی استنتاج ارتقاءیافته (Lifted Inference) در منطق مرتبهاول میپردازد و تلاش میکند محدودیتهای مدلهای کلاسیک را در بیان ویژگیهای ساختاری دادهها (مانند بدونچرخه بودن یا اتصال گراف) برطرف کند. هدف، یافتن شرایطی است که در آن شمارش مدلهای وزنی مرتبهاول (WFOMC) بهصورت چندجملهای و کارا قابلمحاسبه باشد، حتی فراتر از منطق مرتبهاول استاندارد.
مسئلهی اصلی
در یادگیری رابطهای آماری (SRL)، استنتاج احتمالی معمولاً به WFOMC کاهش مییابد، اما این مسئله در حالت کلی #P-کامل است.
پژوهش پیشین نشان داده بود که تنها زیرمجموعهی دومتغیرهی منطق مرتبهاول (FO₂) و نسخهی شمارشی آن (C₂) دامنهقابلارتقاء (domain-liftable) هستند.
این مقاله گام بعدی را برمیدارد:
افزودن ویژگیهای گرافی در سطح ساختار داده (acyclicity، connectivity، tree، forest) به این دامنهها.
⚙️ نوآوری نظری
- روش جدید Counting by Splitting:
- روشی عمومی برای محاسبهی WFOMC با تقسیم حوزههای مستقل و ترکیب نتایج.
- این تکنیک اجازه میدهد ساختارهایی چون گرافهای بدونچرخه و متصل درون چارچوب FO₂ مدل شوند.
- نتایج کلیدی از لمای ۱ و ۲ (در مقاله) منشأ میگیرد که نحوهی ترکیب تفسیرهای جداگانه را بهصورت شمارشی فرمولبندی میکند.
- بسط دامنهی FO₂ و C₂ با محدودیتهای گرافی:
- اگر یکی از روابط در فرمول FO₂ بیانگر گراف بدونچرخه جهتدار (DAG)، گراف متصل، درخت یا جنگل باشد، فرمول همچنان دامنهقابلارتقاء باقی میماند.
- این ویژگیها معمولاً در منطق مرتبهاول قابلبیان نیستند، اما از طریق این چارچوب قابلمدلسازی میشوند.
- اتصال منطق و ترکیبیات شمارشی:
- چارچوب WFOMC بهعنوان ابزار عمومی برای شمارش ساختارهای ترکیبیاتی بهکار گرفته میشود (مثلاً گرافها، شبکههای فیلوژنتیک).
- نویسندگان برای نخستین بار نشان میدهند که میتوان تعداد شبکههای فیلوژنتیک دودویی با (n) گره را در زمان چندجملهای محاسبه کرد.
.

🔬 ساختار پژوهش
- بخش ۲–۳: مرور ادبیات و بازتعریف مفاهیم کلیدی (FOL، FO₂، C₂، WFOMC).
- بخش ۴: معرفی روش اصلی Counting by Splitting با مثالهای گرافیکی.
- بخش ۵–۷: گسترشهای خاص شامل:
- بخش ۵: WFOMC برای گرافهای بدونچرخه (DAG) با استفاده از شمول-استثناء (PIE).
- بخش ۶: مدلسازی گرافهای متصل و جنگلها با محدودیتهای شمارشی.
- بخش ۷: تعمیم به درختهای جهتدار و جنگلهای جهتدار.
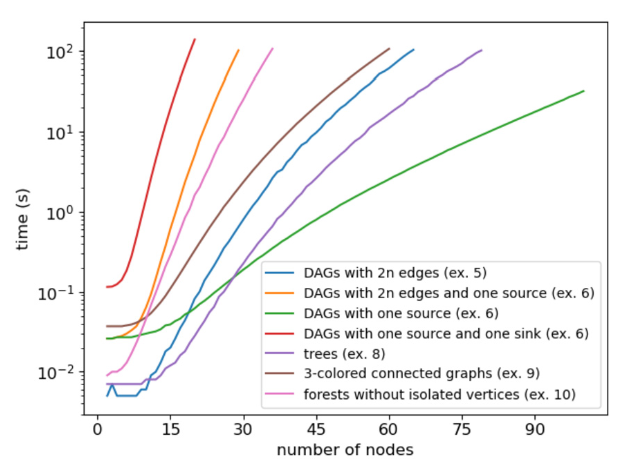
- بخش ۸: تحلیل تجربی کارایی و مقیاسپذیری؛ نتایج تجربی نشان میدهند که روش در سناریوهای واقعی SRL و گرافهای بزرگ نیز کارا است.
📈 نتایج کلیدی
- دامنهقابلارتقاء بودن FO₂ و C₂ در حضور قیود DAG، اتصال و درخت اثبات شد.
- محاسبهی WFOMC در زمان چندجملهای نسبت به اندازهی دامنه (n) امکانپذیر است.
- چارچوب عمومی برای شمارش ترکیبیاتی ایجاد شد که نیاز به طراحی الگوریتمهای خاص را کاهش میدهد.
- پیوندی میان منطق مرتبهاول و ترکیبیات شمارشی مدرن برقرار گردید.
💡 اهمیت و کاربردها
| حوزه | تأثیر مستقیم |
|---|---|
| یادگیری رابطهای آماری (SRL) | بهبود استنتاج احتمالی در مدلهای پیچیده (MLN، PLP) |
| ترکیبیات گرافی | شمارش ساختارهای DAG، درخت، جنگل با روش منطقی عمومی |
| هوش مصنوعی نمادین | افزایش بیانپذیری منطقها فراتر از محدودیتهای FOL |
| زیستشناسی محاسباتی | شمارش شبکههای فیلوژنتیک در زمان چندجملهای |
🧠 جمعبندی مفهومی
این مقاله یک گام نظری بنیادین در جهت رفع شکاف بین منطق استنتاجی و شمارش ساختارهای پیچیده است.
با معرفی «شمارش با تقسیم» (Counting by Splitting)، نویسندگان موفق شدند محدودیتهای کلاسیک منطق مرتبهاول را کنار بزنند و زمینهای برای مدلسازی دقیقتر شبکههای واقعی (مانند شبکههای استنادی یا اجتماعی) فراهم کنند.
دانلود کامل مقاله:


